[BOJ][플2][13504] XOR 합

문제 링크

문제링크

첫 번째 풀이 : XOR

알고리즘

XOR의 특성을 이용한 풀이입니다.

1. a^b^c = c^b^a
2. a^a = 0
3. a^0 = a

즉, 같은 수를 짝수번 xor하면 사라지고, 홀수번 xor하면 그대로입니다.

주어지는 수들을 arr[i]에 저장했다고 했을 때, v[i] = arr[0] ^ … ^ arr[i]으로 정의하겠습니다.
v[i]를 구해두면 값 두개를 xor해서 부분수열을 구할 수 있습니다. 예를 들어 v[4]^v[2] = (a1^a2^a3^a4)^(a1^a2) = a3^a4가 되어 [3,4]의 xor 부분수열을 구할 수 있습니다.

여기까지만 생각해봤을 때 브루트포스로 정답을 구하는 방법은 아래와 같습니다. (시간초과)

cin >> n;
for (i = 0; i < n; i++)
{
    cin >> arr[i];
}
//prefix sum을 구해줍니다. 혹시 모르니 0도 넣습니다.
v.clear();
v.push_back(0);
for (i = 0; i < n; i++)
{
    v.push_back(v[i] ^ arr[i]);
}

for(i=0; i<n; i++){
    for(j=0; j<n; j++){
        ans = max(ans, v[i]^v[j])
    }
}

하지만 N <= 1e5이기 때문에 $N^2$은 1e10이 되어서 100억번의 연산이 필요해서 시간초과가 나옵니다.

조건을 만족하는 연속된 부분 수열을 찾아야하기 때문에 arr[i]은 입력받은 숫자들의 순서가 중요합니다. 하지만 v[i]는 v에 속한 두 값을 골라서 xor을 했을 때 xor 부분 수열의 길이의 개념을 도출할 수 있기 때문에 순서가 더이상 의미를 가지지 않습니다. 그래서 정렬을 합니다.

v[i]의 값이 정렬이 되었다고 생각하고 예를 들어보겠습니다.

[0] : 0000 
[1] : 0001
[2] : 0010
[3] : 0011
[4] : 0011
[5] : 0100
-------------------최상위 비트 없는/있는 기준
[6] : 1000
[7] : 1101

n이 7이라고 할 때, XOR 합이 크기 위해서는 XOR 결과의 각 비트가 1이되도록 부분 수열을 구성해야 합니다. 예를 들어 v[6]^v[7]은 최상위 비트 1000이 사라지기 때문에 피해야하는 조합입니다. 즉, 최상위 비트가 있는 v[i]와 최상위 비트가 없는 v[j]를 골라서 XOR해야합니다. 최상위 비트는 모든 v[i]의 값이 같지만 않다면 항상 구할 수 있습니다.

위와 같은 경우 XOR 합이 가장 큰 경우는 다음과 같을 것입니다.

// 총 12번 연산
for(i = v[6] ~ v[7]){
    for(j = v[0] ~ v[5]){
        ans = max(ans, i^j)
    }
}

하지만 여전히 v.size()는 n과 같기 때문에, 최상위 비트 유무의 기준이 절반이라면 O(5만*5만) = O(25억)이라서 여전히 시간초과입니다. 하지만 최상위 비트 유무로 나누었기 때문에 시간 복잡도가 많이 줄었습니다. 같은 방법을 더 적용해보면 시간 초과를 피할 수 있습니다.

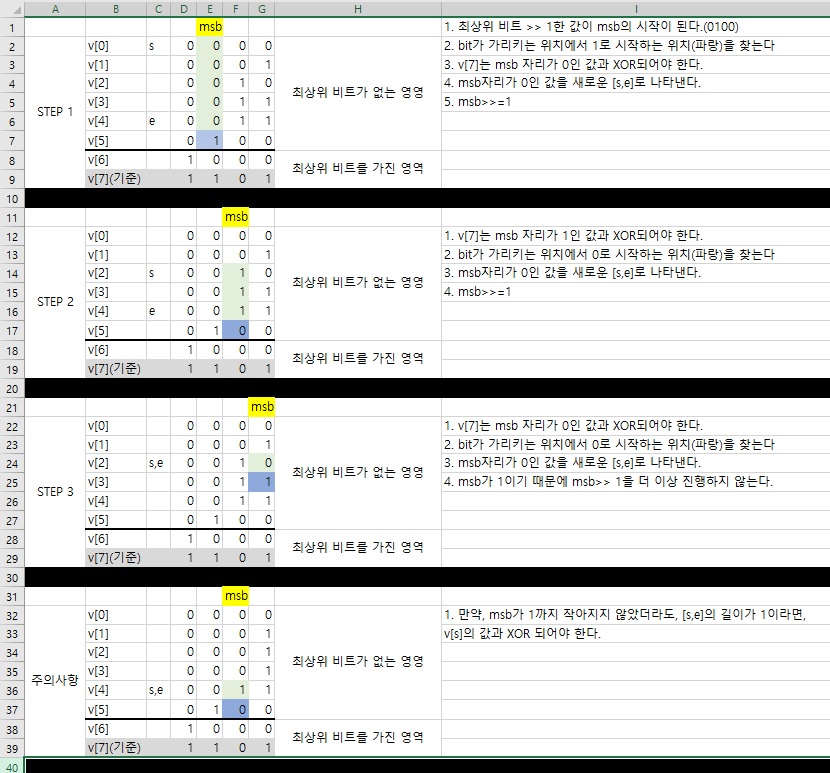
여기서 v[6]은 최상위비트(1000) 바로 아래의 비트(0100)가 0입니다. 따라서 0100 자리의 비트는 1인 것(v[0]~v[4])과 XOR 되어야 큰 값을 구할 수 있습니다. [7]는 0100자리의 비트가 1이므로, 0100자리의 비트가 0인 값(v[5])과 xor 되어야 합니다.

[0] : 0000 // s: [7]의 0100자리의 1을 살리기 위해서 xor 되어야 하는 영역의 시작
[1] : 0001 //
[2] : 0010 //
[3] : 0011 //
[4] : 0011 // e: [7]의 0100자리의 1을 살리기 위해서 xor 되어야 하는 영역의 끝
[5] : 0100 //
-------------------최상위 비트 없는/있는 기준
[6] : 1000
[7] : 1101

이렇게 구분해서보면 시간 복잡도를 더 줄일 수 있습니다.

// 총 6번 연산
if(i = v[6]){
    for(j = v[5]){
        ans = max(ans, i^j);
    }
}else if(i = v[7]){
    for(j = v[0] ~ v[4]){
        ans = max(ans, i^j);
    }
}

정답코드

#include <bits/stdc++.h>
using namespace std;

using ll = long long;
using pii = pair<int, int>;

const int MAX = 100'010;

int arr[MAX];
vector<int> v;
int n, m;


//[s,e] : 최상위 비트가 없는 구간
//[idx,) : 최상위 비트가 있는 구간
// 최상위 비트가 0000 1000일때 bit는 0000 0100부터 시작
// bit가 0000 0100일때 0000 010?과 0000 011?로 나누어서 생각
/**
s     : 0001
      : 0010
e     : 0100
value : 1000
value의 값은 최상위 비트를 가진 값들이 들어온다.
bit는 value의 최상위 비트 위치에서 >>가 1번 이상된 값이 들어온다.
value가 1000일 때 bit는 0100, 0010, 0001까지 들어올 수 있다.
*/
int binary_search(int s, int e, int value, int msb) {
    int ts = s;
    int te = e;
    
    
    int idx = e + 1; 
    int mid = 0;

    // 구간의 크기가 1이하이거나, 최하위 비트까지 모두 살펴본 경우
    if (s >= e || msb == 1) return v[s] ^ value;

    //이진탐색으로 msb부분이 0인 구간과 1인 구간을 나눠줍니다. 
    // [s, idx-1] 구간은 010? 상태인 구간, [idx, e] 구간은 011?인 구간입니다.
    while (ts <= te) {
        mid = (ts + te) / 2;
        if (v[mid] & msb) { // bit번째 비트가 1인가?
            idx = mid;
            te = mid - 1;
        }
        else {
            ts = mid + 1;
        }
    }
    // 이제 idx에는 msb 자리의 비트가 1인 가장 작은 index가 저장되어 있다.

    // value의 msb 자리의 bit가 1인 경우와 0인 경우 
    if (value & msb) return binary_search(s, idx - 1, value, msb / 2);
    else return binary_search(idx, e, value, msb / 2);
}

int main()
{
    freopen("input.txt", "r", stdin);
    ios_base::sync_with_stdio(0); cin.tie(0);
    int tc = 0; cin >> tc;
    while (tc--) {
        cin >> n;
        for (int i = 0; i < n; i++) {
            cin >> arr[i];
        }
        v.clear();
        v.push_back(0);
        // v[i] : v[0...i]까지의 XOR 저장
        for (int i = 0; i < n; i++) {
            v.push_back(v[i] ^ arr[i]);
        }
        // XOR의 값을 저장했으므로 순서는 중요하지 않게 되었다.
        // 왜냐하면 v에 저장된 값 두 값의 XOR 값이 가장 큰 것만 찾으면 된다.
        sort(v.begin(), v.end());
        // 전체 부분 행렬을 default 정답으로 저장
        int ans = v.back();
        // 4바이트 기준 양수의 최상위 비트는 1 >> 30으로 구한다.
        // 0100'0000 0000'0000 0000'0000 0000'0000 
        int msb = 1 << 30; 
        // 최상위 비트를 찾는다.
        while (!(v[v.size() - 1] & msb)) msb >= 1;
        // 최상위 비트가 있는 범위와 없는 범위의 기준을 찾는다.
        int i = 0;
        for (i = v.size() - 1; i >= 0; i--) {
            if (!(v[i] & msb)) break;
        }
        // [0, idx-1]까지는 최상위 비트가 없는 구간
        // [idx, )는 최상위 비트가 있는 구간
        int idx = i + 1;
        for (int i = v.size() - 1; i >= 0; i--) {
            // 최상위 비트에서 1비트 shift
            // msb/2는 msb>>1과 같다
            ans = max(ans, binary_search(0, idx - 1, v[i], msb/2));
        }
    }
    return 0;
}

Success Notice: 수고하셨습니다.