[Edit distance] 편집거리

정의

두 문자열의 유사도에서 다음 두 개의 개념이 나온다.

• Hamming distance: 단순히 틀린 글자수

이것은 두 문자열에 대해서 같은 index에 있는 모든 문자들을 비교하면 된다.

• 편집 거리 (Edit distance)

문자열 A를 문자열 B로 바꾸기 위해서는 다음 연산이 몇 번 필요한가?

1. 한 글자 지우기
2. 한 글자 넣기
3. 한 글자 다른 글자로 바꾸기

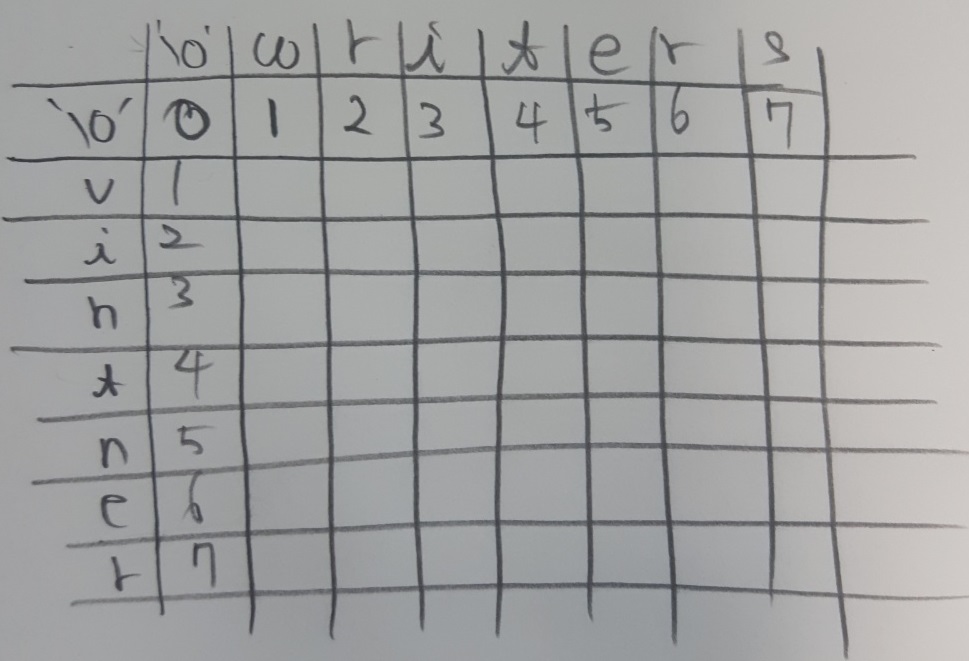
이번에는 DP 테이블의 한 칸은 이런 의미를 가집니다. 문자열 A의 0~i번째와 문자열 B의 0~j까지의 편집거리. 따라서 공백 문자를 w로 바꾸기 위해서는 3번 연산이 1번, “공백 문자+w”를 “wr”로 바꾸기 위해서는 3번 연산 1번 그리고 2번 연산 1번을 해야합니다. 그런데 DP 알고리즘에서는 이전까지 구한 값을 현재의 값을 구하는데 사용합니다. D[i][j+1]의 값을 구할 D[i][j]의 값이 필요한데 D[i][j]에서 D[i][j+1]로 옮겨가는 과정은 다음과 같이 이해할 수 있습니다. A[0:i]를 B[0:j]로 바꾸는데 D[i][j]번 만큼의 연산이 걸렸습니다. 이제 B[j]의 문자열을 추가합니다. A[0:i]문자열을 B[0:j+1]로 바꾸기 위해서는 D[0:j] 이후에 새롭게 추가된 하나의 문자만 확인하면 됩니다.

반대로 생각하면 문자열 D[i+1][j+1]을 만드는 것은 세 가지 가능성이 있습니다. 이는 아래 그림의 (1)~(4)를 보면서 설명하겠습니다.

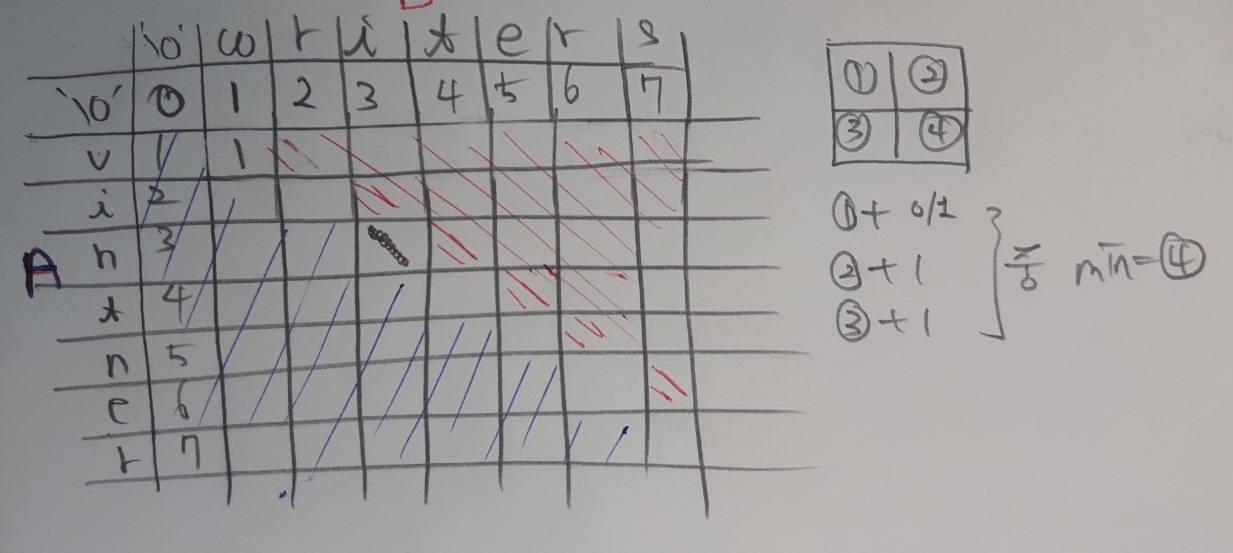
(4)번 자리에 있는 값을 알고 싶습니다. 이 값이 될 수 있는 첫 번째 가능성은 (3)자리에 있는 값에서 +1을 하는 것입니다. +1은 새롭게 추가된 문자열과 일치 시키기 위해서 다른 문자열에서 2번 연산을 1번 수행하는 것을 의미합니다. (2)자리에서도 (3)과 같은 의미로 (2)+1의 값이 (4)가 가질 수 있는 두 번쨰 값입니다. 마지막으로 (4)가 될 수 있는 가능성은 (1)에서 나옵니다. 문자열 A[0:i]와 B[0:j]를 똑같이 만드는데 편집거리 N만큼 소요돼었습니다. 다음으로 두 문자열에 같은 문자가 추가될 수도 있고(편집거리 +0) 다른 문자가 추가될 수도 있습니다(편집거리 +1). 따라서 (4)가 가질 수 있는 값은 N+1 또는 N + 0 입니다.

즉, (4) 는

1. (2)+1
2. (3)+1
3. (1)+1
4. (1)+0

의 값 중 하나를 가질 수 있습니다. 최소 편집 거리를 구하고 싶으므로 이들 중 최소값이 (4)의 값입니다. 쉽게 생각하면 D[i][j]의 값은 A[i]와 B[j]가 같으면 (1) 이고, A[i]와 B[j]가 다르면 min((1),(2),(3)) + 1 입니다.

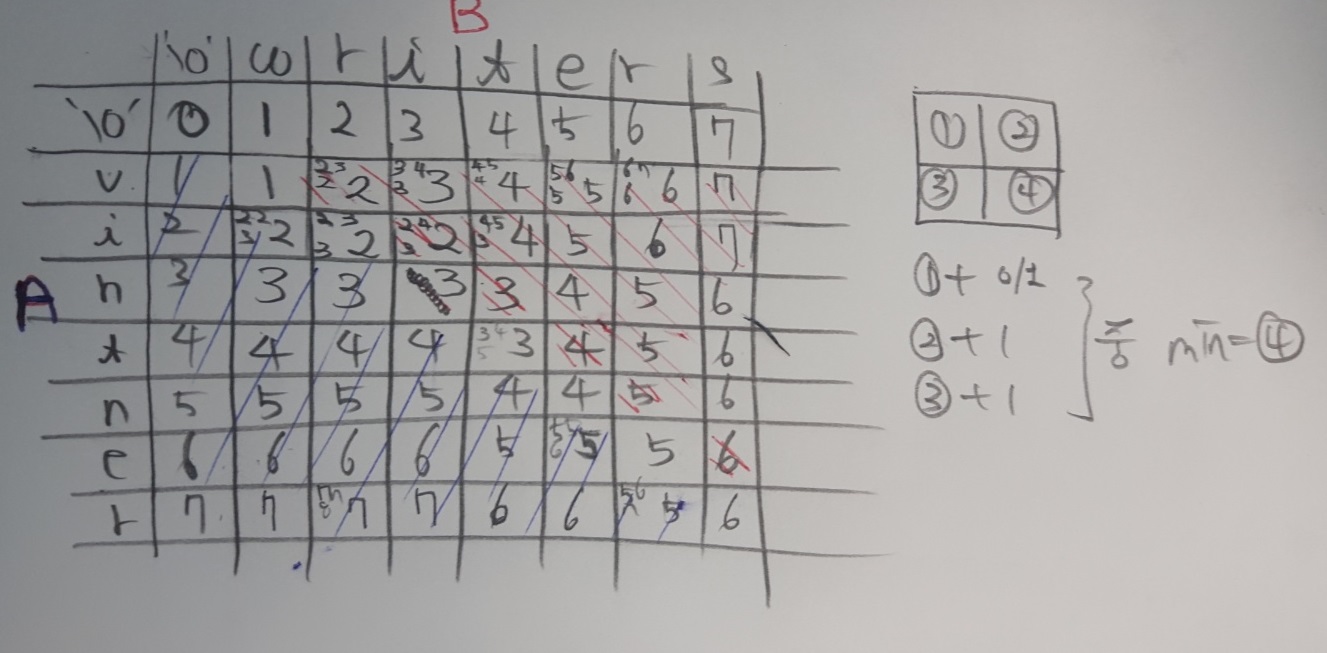
테이블을 채우면 위와 같이 됩니다.

어떻게 바꾸면 문자열 A를 B로 바꿀 수 있는지(혹은 그 반대)는 LCS 포스팅과 마찬가지로 화살표를 사용하면 됩니다. 어떻게 (4)의 값을 구했는지 기억해두면 이를 찾아갈 수 있습니다.

//Recursive로 푸는 코드
int editDist(string str1 , string str2 , int m ,int n)
{
    //문자열 str2를 st1로 바꾸는 과정
    if (m == 0) return n;
    if (n == 0) return m;
    if (str1[m-1] == str2[n-1])
        return editDist(str1, str2, m-1, n-1);
    return 1 + min ( editDist(str1, str2, m, n-1), // Insert : 문자열 str2의 뒤에 문자 하나를 추가
                     editDist(str1, str2, m-1, n), // Remove : 문자열 str1의 앞에서 문자 하나를 삭제
                     editDist(str1, str2, m-1, n-1) // Replace : 
    );
}

//DP로 푸는 코드
int editDistDP(string str1, string str2, int m, int n)
{
    int dp[m+1][n+1];
    for (int i=0; i<=m; i++) {
        for (int j=0; j<=n; j++) {
            //최상위 row 채우기
            if (i==0) dp[i][j] = j; // Min. operations = j
            //최좌위 col 채우기
            else if (j==0) dp[i][j] = i; // Min. operations = i
            //마지막에 추가한 문자 두 개가 같은 경우
            else if (str1[i-1] == str2[j-1]) dp[i][j] = dp[i-1][j-1];
            //마지막 두 개가 다른 경우
            else
                dp[i][j] = 1 + min( dp[i][j-1], // Insert
                                    dp[i-1][j], // Remove
                                    dp[i-1][j-1]); // Replace
            }
    }
    return dp[m][n];
}

int main()
{
    string str1 = "sunday";
    string str2 = "saturday";
    cout << editDist( str1 , str2 , str1.length(), str2.length());
    return 0;
}