[Idea] Maximum Square 구하기
문제
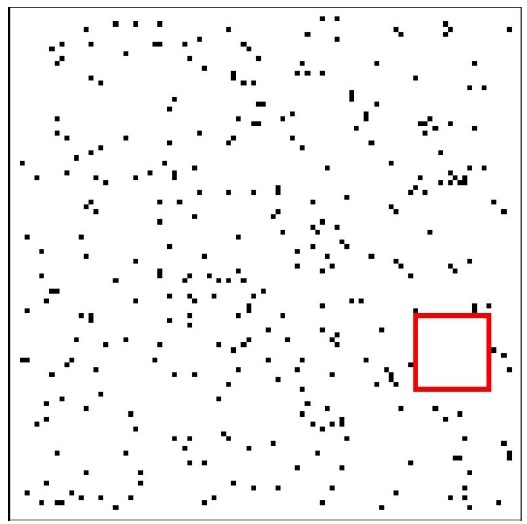
n x n 칸이 주어져 있고, 각 칸은 흰색 아니면 검은색이다. 흰색으로만 이루어진 가장 큰 정사각형을 찾으시오.
풀이 : DP
이 문제는 , 모든 DP 문제가 다 그렇지만, DP 테이블에서 각 셀이 가지는 의미를 정의하는 것이 매우 중요합니다.
D[x][y]: (x, y)가 가장 오른쪽 아래 꼭지점인 가장 큰 정사각형의 한 변의 길이
- (x, y)가 검은 색
- D[x][y] = 0
- (x, y)가 흰색
- x = 1 이거나 y = 1 : D[x][y] = 1
- 그 외의 경우 : D[x][y] = min(D[x-1][y-1], D[x-1][y], D[x][y-1]) + 1
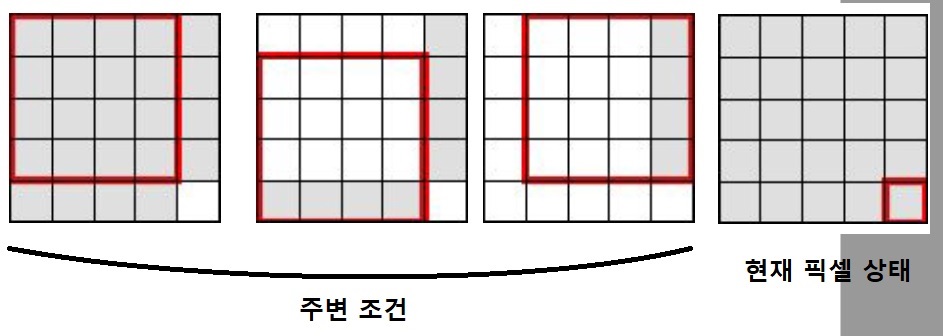
주변에서 공통적으로 구할 수 있는 가장 작은 정사각형의 크기에서 현재의 좌표까지 정사각형에 넣을 수 있으면 +1이 됩니다.
시간 복잡도
모든 점을 방문하면서 $O(N^{2})$ 주변의 3개의 좌표를 검사하므로 $O(1)$ 최종적인 시간 복잡도는 $O(N^{2})$입니다.

Leave a comment