[아이디어] 주식
문제
n일간의 주식 가격이 n개의 서로 다른 정수로 주어져 있다.
17, 30, 42, 15, 20, 50, 10, 25
이 때 한 번 주식을 사고 한 번 팔 수 있을 때, 얻을 수 있는 최대 이익을 구하시오.
위 예에서 15에 사고 50에 팔면 35의 이익을 얻을 수 있고, 이 값이 최대이익이다.
풀이 : 한 번 사고 파는 경우
당연하게도 주식을 산 날에는 바로 되팔 수 없고, 주식을 사기 전에 미리 팔 수도 없다. 산 날짜의 이후에 팔아야한다.
매 날짜마다 그날 그날의 이익을 구하고 이들의 최대값을 찾으면 된다.
매 날짜마다 그날의 이익 = 현재의 가격 - 주식을 산 날짜의 가격이므로, 현재날짜가 되기 전에 가장 가격이 쌀 때 사면 된다.
즉, 매 날짜마다 그날의 최대 이익 = 현재의 가격 - 시작부터 어제까지 가장 가격이 낮은 날의 가격
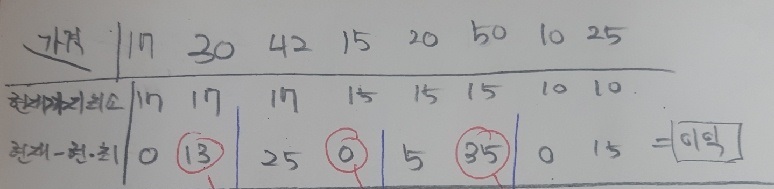
그림에서 두 번째 줄은 현재까지 최소를, 세 번쨰 줄은 현재-현재까지 최소를 나타낸다.
현재-현재까지 최소는 그날에 판다면 얻을 수 있는 최대 이익을 의미하기 때문이다. 이를 구하면서 최대값을 갱신하면서
기록한다면 $O(N)$만에 한 번 사고 팔 때의 최대 이익을 구할 수 있다.
풀이 : 두 번 사고 파는 경우
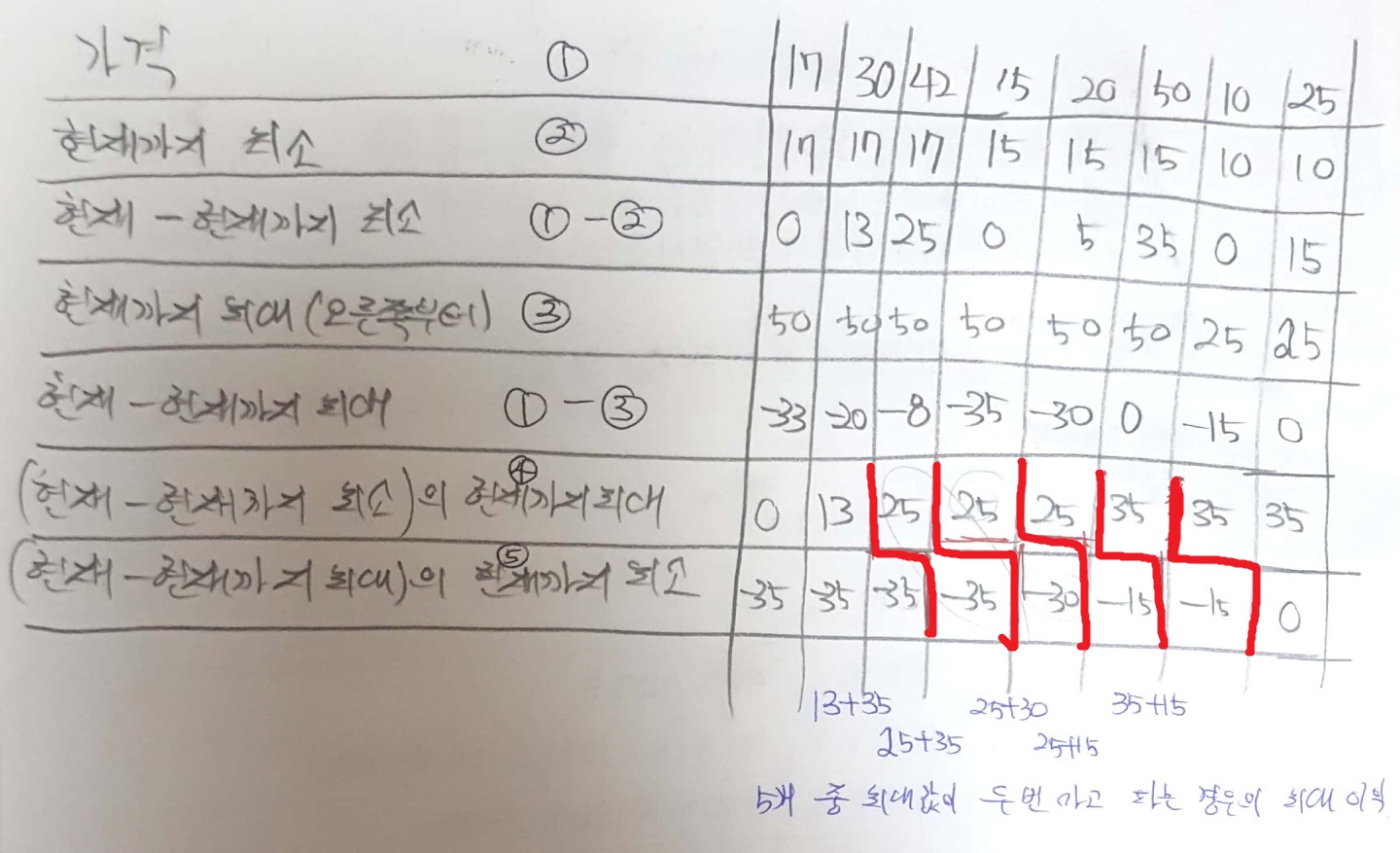
문제의 조건에 따라서 구매-판매-구매-판매 순서대로 진행해야 한다.
- 가격 : 해당 날짜의 주식 가격
- 현재까지 최소 : 왼쪽부터 읽으면서 지금까지 발견한 최소 가격
- (1) - (2) : 해당 날짜에서 얻을 수 있는 최대 이익 ( 한 번 사고 한 번 파는 경우의 답 )
- 현재까지 최대 : 오른쪽부터 읽으면서 지금까지 발견한 최대 가격
- (1) - (3) : 오늘 사서 최대 날짜에 판다면 얻을 수 있는 최대 이익 * -1
- 해당 날짜 이전에 사서 해당 날짜에 파는 경우 얻을 수 있는 최대 이익
- 해당 날짜에 사서 최대 가격 날짜에 파는 경우 얻을 수 있는 최대 이익 * -1
위 7가지를 구하고, 빨간색으로 표시된 가능한 모든 경계마다 6,7번째 줄의 왼쪽에 있는 값의 절대값을 더하면 해당 날짜에서의 최대 이익을 얻을 수 있다.
예를 들어서 가장 왼쪽의 13과 -35의 절댓값을 더하면 13 + 35 = 48이다. 13은 둘 째날 이전에 사서 둘 째날에 팔았을 때 얻을 수 있는 최대 이익을 의미한다. -35는 셋 째날에 사서 가장 비쌀 때 팔아서 얻을 수 있는 최대 이익 * -1를 의미한다. 빨간색 경계는 구매 - 판매 - 구매 - 판매를 번갈아 가면서 해야하는 조건에 따라서 위 그림에서 표시된 경계 외에는 더 고려할 필요가 없다.
경계 좌우의 빨간 원의 합인 최종이익을 구하고 이들의 $MAX$값을 찾으면 된다.
시간 복잡도
$O(N)$에 풀 수 있다.

Leave a comment